Swish - a Self-Gated Activation Function

22 Oct 2017

Introduction

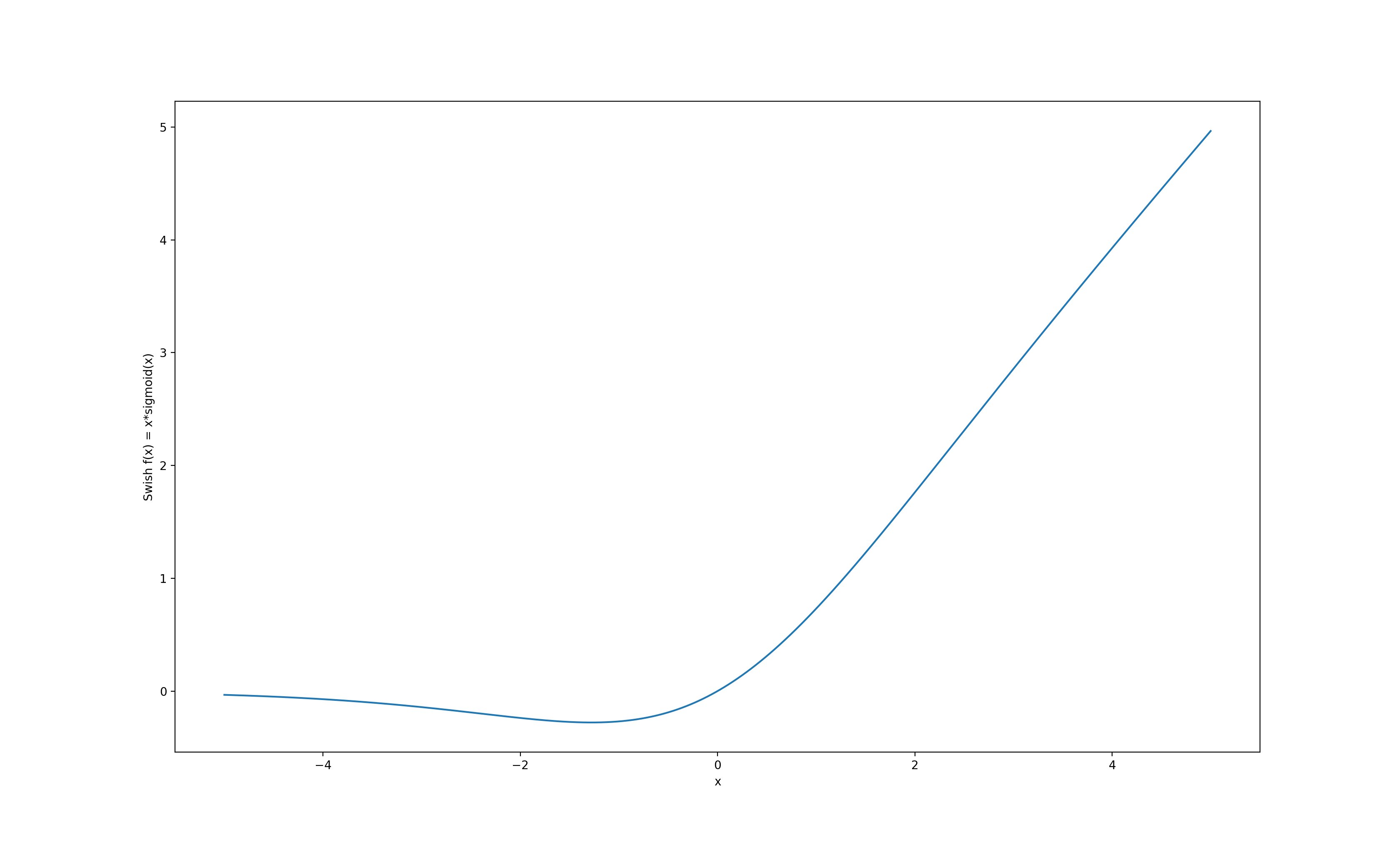
The paper presents a new activation function called Swish with formulation f(x) = x.sigmod(x) and its parameterised version called Swish-β where f(x, β) = 2x.sigmoid(β.x) and β is a training parameter.
The paper shows that Swish is consistently able to outperform RELU and other activations functions over a variety of datasets (CIFAR, ImageNet, WMT2014) though by small margins only in some cases.
Link to the paper

Smooth, non-monotonic function.
Swish-β can be thought of as a smooth function that interpolates between a linear function and RELU.
Uses self-gating mechanism (that is, it uses its own value to gate itself). Gating generally uses multiple scalar inputs but since self-gating uses a single scalar input, it can be used to replace activation functions which are generally pointwise.
Being unbounded on the x>0 side, it avoids saturation when training is slow due to near 0 gradients.
Being bounded below induces a kind of regularization effect as large, negative inputs are forgotten.
Since the Swish function is smooth, the output landscape and the loss landscape are also smooth. A smooth landscape should be more traversable and less sensitive to initialization and learning rates.

Swish is much more complicated than ReLU (when weighted against the small improvements that are provided) so it might not end up with as strong an adoption as ReLU.